My general area of research is Computational Fluid Dynamics (CFD) and Numerical Methods for Partial Differential Equations. More specifically my research encompasses developing efficient Higher Order Compact (HOC) schemes to numerically simulate incompressible viscous flows governed by the Navier-Stokes (N-S) equations.
We have developed numerous differential equation based HOC schemes for the two-dimensional (2D) steady-state and transient Convection-Diffusion equations which has been successfully implemented on the N-S equations both in the primitive variable and the streamfunction-vorticity formulations. These schemes are well-equipped to handle problems in rectangular as well as curvilinear coordinates, again both in uniform as well as nonuniform grids. We have also applied them to flows in porous media involving both heat and mass transfer. Recently we have developed a super-compact HOC scheme for the three-dimensional (3D) Convection-Diffusion equation which has been implemented to resolve flows governed by the 3D N-S equations as well. Here are some cool pictures of the simulations for the 3D lid-driven cavity flow at Re=100 computed on a 65x33x65 grid.
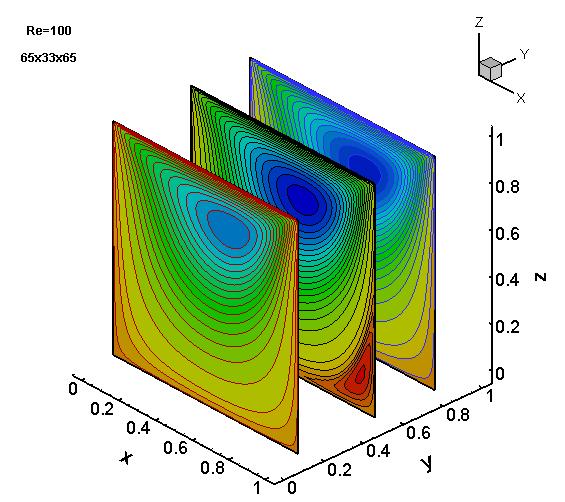
Projection of the stream-function on x-z plane at y=0.11, 0.5 and 0.8.
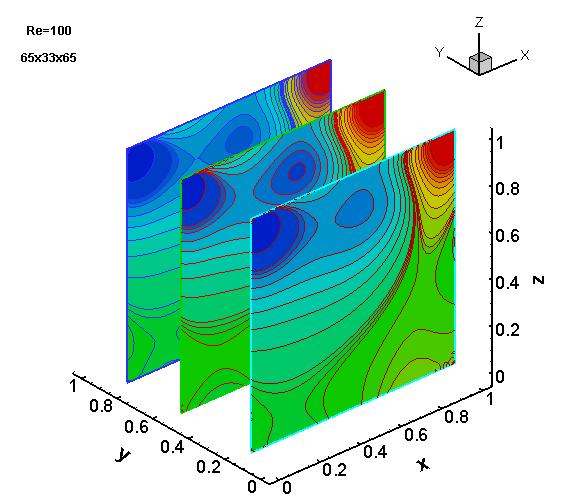
Projection of pressure on x-z plane at y=0.11, 0.5 and 0.8.
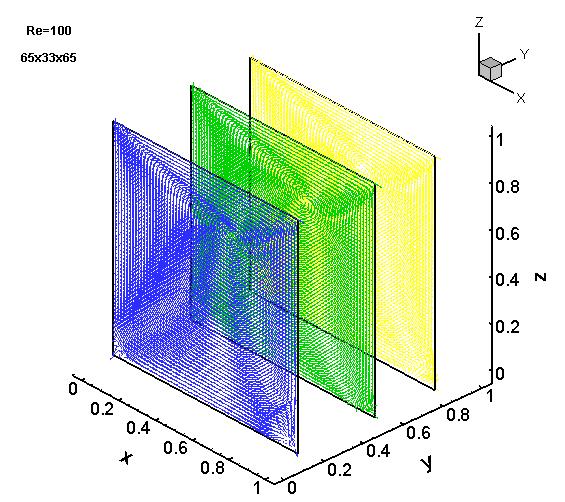
Vector plots on x-z plane at y=0.11, 0.5 and 0.8.
In addition to this, we have also developed a ψ-v formulation for the 2D N-S equations that uses an infinite series based HOC scheme. Recently we have successfully extended this approach to curvilinear coordinates ; we have also extended the scheme on rectangular domains to transient flows. (see the following simulations: two-sided lid-driven cavity problem at Re=800, the motion past a circular cylinder problem at Re=80 and periodic flow for the motion past a square cylinder at Re=200.) Currently we are working on the 3D version of this approach.
The two-sided lid-driven cavity at Re=800 with aspect
ratio 1.96:
the streamlines: top: numerical, bottom: experimental
Streamline evolution for the flow past a
circular cylinder at Re=1000: (a) t=2.5, (b)t=2.75, (c) t=3.00, (d) t=3.25 (e)
t=3.75 and (f) t=4.00.
Motion
past a square cylinder at Re=200: the streamfunction contours depicting the
wake behind three successive instants of
time over one vortex shedding period.
Motion
past a square cylinder at Re=200: the vorticity contours depicting the wake
behind three successive instants of
time over one vortex shedding period.
Recently, we have had some tremendous success with the biharmonic formulation of the N-S equations on irregular geometries. Here is a cool simulation of the streaklines for the laminar flow past an impulsively started circular cylinder at Re=200.
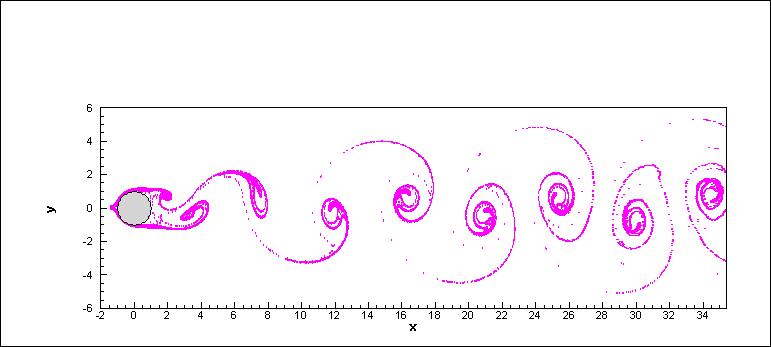
For an animated version of the von Kármán vortex street behind a circular cylinder at Re=50 click here and Re=200, click here. With this formulation we have also successfully simulated the flow past an impulsively started NACA 0012 airfoil in the laminar range. Following are the simulation for Re=1000 and angle of attack 34 degrees.
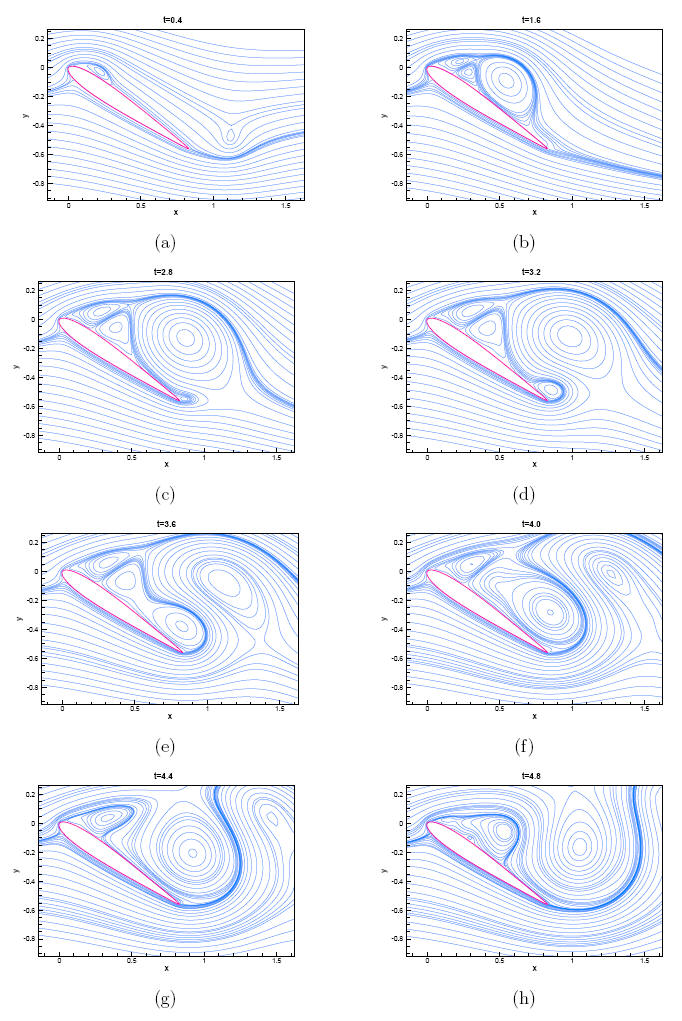
At present, we are trying to club together the HOC methodology to other existing CFD tools to develop even more efficient schemes. One of such efforts has been to club our HOC approach to the immersed interface method in Cartesian grids to capture discontinuities and to solve interface problems. We are also in the process of extending the existing HOC methodology to adaptive grids and local defect correction strategy. More recently, we are moving in the direction of applying the HOC methodology to mathematical approaches in financial and biological problems.
I am also interested in the implementation of advanced iterative solvers like Conjugate Gradient (CG), BiConjugate Gradient (BiCG), BiConjugate Gradient Stabilised (BiCGStab), Hybrid BiConjugate Gradient Stabilised (BiCGStab2) methods as well as Multigrid methods. All along, I have been using them quite extensively in my computer codes.
To know more about my research, feel free to look at some of my publications. All of my published papers are available on request; you can write to me at the following e-mail addresses: jiten [*AT] iitg.ernet.in or jiten_kalita [*AT] yahoo.co.in