


Next: About this document ...
Up: tut1
Previous: tut1
- Griffiths (2.3)
-
![$\frac{\lambda}{4\pi\epsilon_0}[(L/z\sqrt{L^2+z^2}){\mathbf k}
-(1/z\sqrt{L^2+z^2}-1/2z){\mathbf i}]$](img1.png)
- Griffiths (2.5)
-
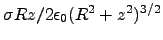
- Griffiths (2.6)
-
![$\frac{\sigma}{2\epsilon_0}[1 - z/\sqrt{R^2+z^2}] $](img3.png)
- Griffiths (2.9)
- (a)
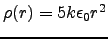 ;(b)
;(b)

- Griffiths (2.15)
-
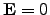 if
if 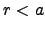 .
.
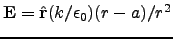 if
if 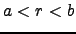 .
.
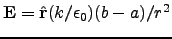 if
if 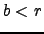 .
. 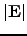 is
increasing at
is
increasing at 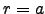 , has a maximum at
, has a maximum at 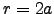 if
if 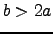 .
.
- Griffiths (2.18)
-
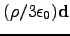
- Griffiths (2.26)
-
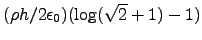
- Jackson (1.3)
- (a)
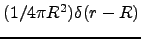 ;(b)
;(b)
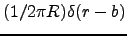 (c)
(c)
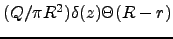 (d)
(d)
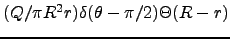
- Jackson (1.4)
-
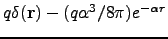
Charudatt Kadolkar
2007-01-30