


Next: About this document ...
Up: tut2
Previous: tut2
- Jackson (1.7)
- Here we assume that the conducting wires are far apart, hence the charge
is uniformly distributed over the surface of each wire. Hence the potential
is given by
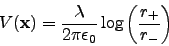 |
(1) |
Thus potential of the two wires are
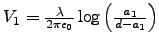 and
and
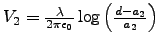 . capacitance is
. capacitance is
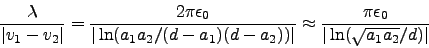 |
(2) |
- Jackson (1.10)
- By integral formula (Eq 1.36 of Jackson) for potentials
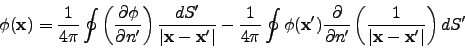 |
(3) |
Since
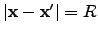 and
and
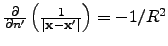 , the first integral vanishes
by Gauss law and second integral is simply the average value of the potential on the surface of the sphere.
, the first integral vanishes
by Gauss law and second integral is simply the average value of the potential on the surface of the sphere.
- Jackson (1.12)
- Hint: Use Green's second identity. Remember
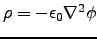 and
and
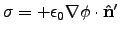 .
.
- Jackson (2.2)
- (a) The image charge of magnitude
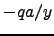 must be kept outside at a distance
must be kept outside at a distance 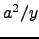 . (d) All you need to do is add a constant to the result of part (a). The induced charge densities are same!
. (d) All you need to do is add a constant to the result of part (a). The induced charge densities are same!
- Jackson (2.3)
- (a) Equipotential surfaces are shown in the figure.
Figure 1:
Jackson 2.3 (a) Equipotential surfaces.(b) Charge density along x axis
|
|
(b) The required plots.
- Jackson (2.4)
- (a) The force on charge
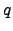 is given by
is given by
![\begin{displaymath}
\v{F}_q = \frac{q^2\v{\hat{k}}}{4\pi\epsilon_0}\left[
\frac{d+R}{d^2} - \frac{dR}{(d^2-R^2)^2} \right]
\end{displaymath}](img15.png) |
(4) |
Equating magnitude of the force to zero, we get three real solutions for
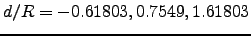 . Only one solution is outside the sphere.
. Only one solution is outside the sphere.
- Jackson (2.7)
- The required Green's Function is
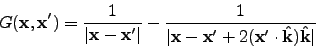 |
(5) |
In cylindrical coordinates,
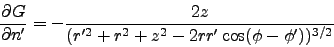 |
(6) |
Then, the potential at any point (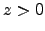 ) is given by
) is given by
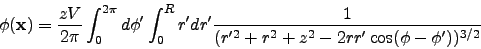 |
(7) |



Next: About this document ...
Up: tut2
Previous: tut2
Charudatt Kadolkar
2007-02-05
![\begin{displaymath}
\v{F}_q = \frac{q^2\v{\hat{k}}}{4\pi\epsilon_0}\left[
\frac{d+R}{d^2} - \frac{dR}{(d^2-R^2)^2} \right]
\end{displaymath}](img15.png)
![\begin{displaymath}
\v{F}_q = \frac{q^2\v{\hat{k}}}{4\pi\epsilon_0}\left[
\frac{d+R}{d^2} - \frac{dR}{(d^2-R^2)^2} \right]
\end{displaymath}](img15.png)