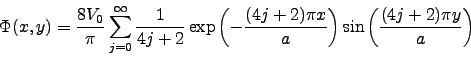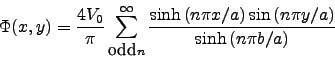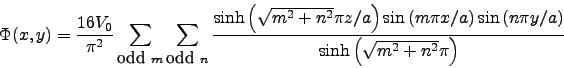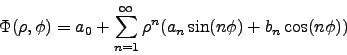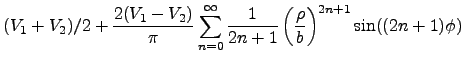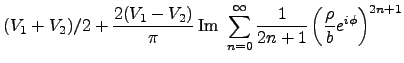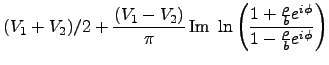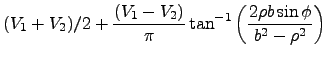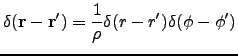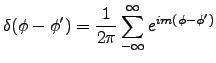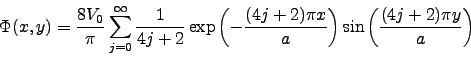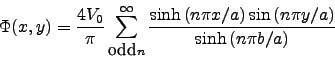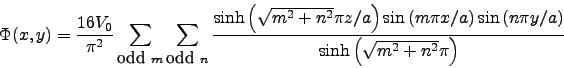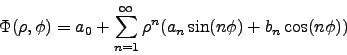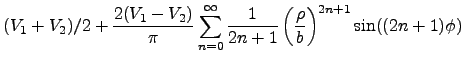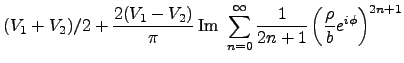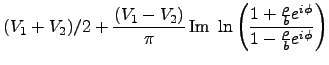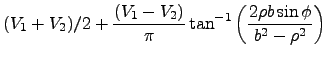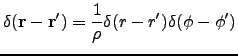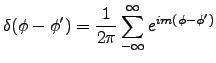Next: About this document ...
Up: tut3
Previous: tut3
- Griffiths (3.12)
-
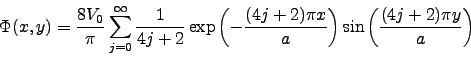 |
(1) |
- Griffiths (3.14)
-
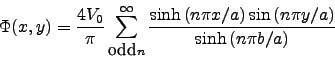 |
(2) |
- Griffiths (3.15)
-
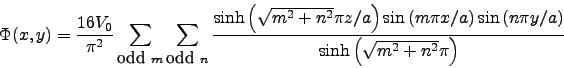 |
(3) |
- Jackson (2.13)
- (Unfortunately I chose wrong geometry. Change
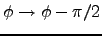 to get Jackson's answer). For
to get Jackson's answer). For 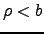 ,
the general solution is
,
the general solution is
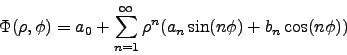 |
(4) |
Boundary conditions:
Then,
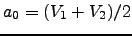 ,
, 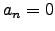 for all even
for all even 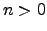 ,
,
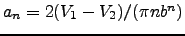 for all odd
for all odd 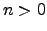 .
. 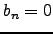 for all
for all 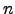 . Thus,
. Thus,
And the charge density is
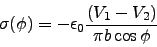 |
(11) |
- Jackson (2.14)
-
- Jackson (2.17)
- Use following identities to prove the result:
| |
|
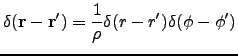 |
(12) |
| |
|
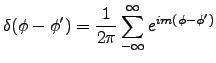 |
(13) |
To find 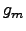 when
when 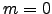 , choose
, choose
But then 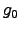 does not vanish as
does not vanish as
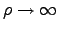 . When can you use this Green's
Function?
. When can you use this Green's
Function?
- Jackson (2.20)
- Use the Green's Function derived above.



Next: About this document ...
Up: tut3
Previous: tut3
Charudatt Kadolkar
2007-02-21